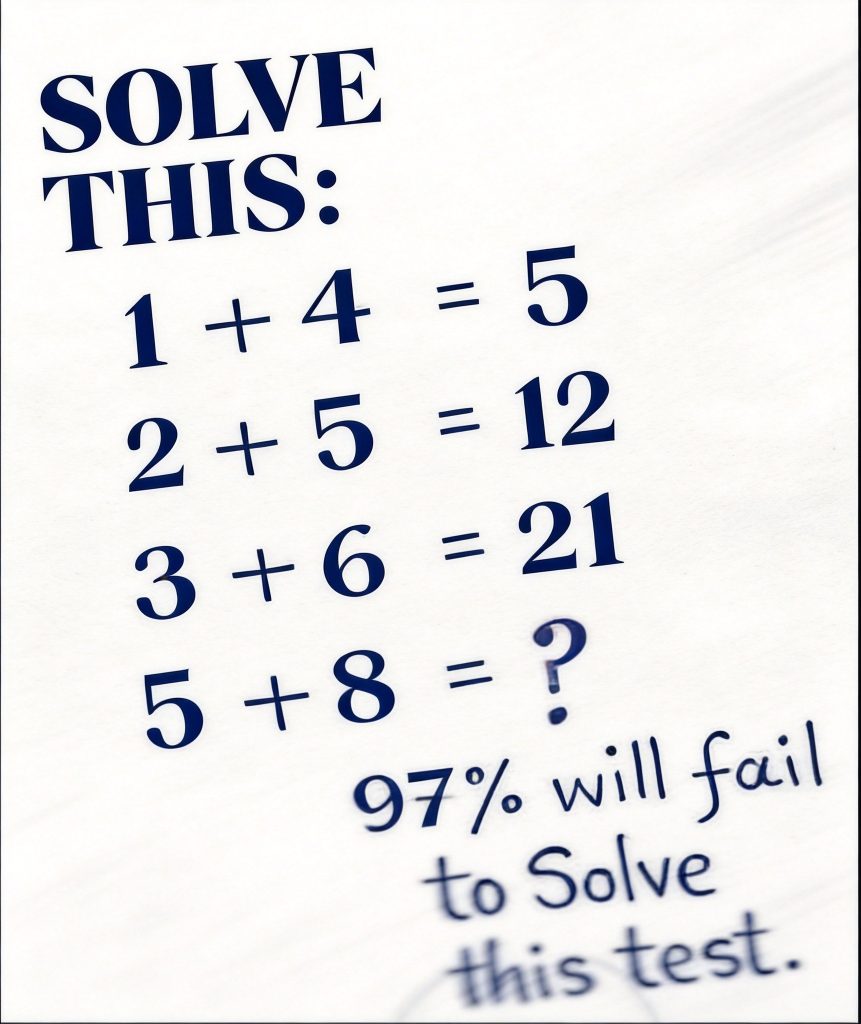Engaging with Mathematical Puzzles in the Modern Era
As we navigate through an increasingly digital landscape, the way we engage with math has transformed significantly. For many individuals, the traditional experience of sitting in a classroom, surrounded by textbooks and solving endless math problems, feels like a relic of the past. While some find joy and intrigue in numbers, others experience anxiety or disinterest at the mere mention of mathematics. However, the rise of the internet has birthed a new platform for mathematical interaction through engaging brain teasers, puzzles, and logic challenges. What stands out is the ability of these puzzles, though often deceptively simple, to captivate our minds for extended periods, sparking lively debates and discussions across social media platforms and dedicated online communities. These digital spaces have become vibrant hubs for math enthusiasts and novices alike, offering a plethora of challenges that cater to a wide array of skill levels.
One recent puzzle that has garnered significant attention is a sequence that initially appears to be elementary: 1 + 4 = 5, 2 + 5 = 12, 3 + 6 = 21, 5 + 8 = ? At a cursory glance, this seems to be a basic arithmetic challenge that anyone could tackle. Yet, as one delves deeper, trying to apply conventional arithmetic rules leads to confusion. The results deviate drastically from standard mathematical outcomes, prompting the question: What lies beneath the surface of this puzzle? The allure of this sequence stems from its unpredictability and the necessity to think outside the box, steering clear of normal addition guidelines and exploring hidden patterns or relationships. This puzzle not only tests mathematical skills but also challenges our ability to think creatively and critically.
Why Mathematical Puzzles Spark Interest
This puzzle serves as a quintessential example of what mathematicians often refer to as a “pattern problem” or a “sequence puzzle.” The true challenge does not lie in performing arithmetic accurately but in uncovering the underlying rules that dictate how the numbers interact. Such puzzles appeal to a diverse audience, merging logical reasoning with creative thinking—qualities that extend beyond the realm of mere mathematics. The puzzle’s popularity is evident on platforms like Reddit, Quora, and various brain-teaser websites, where thousands of users actively engage in solving it. Approaches vary widely; some individuals employ analytical methods, experimenting with different mathematical operations such as multiplication or division, while others adopt a more imaginative perspective, interpreting the “+” not just as addition but as an indication of a sequence-based rule or cumulative operation. This diversity in interpretation invites an enriching dialogue about mathematical thought and problem-solving strategies.
Diverse Approaches to Solving the Puzzle
To fully appreciate the puzzle’s complexity and divisiveness, it is essential to explore some of the most common interpretations:
1. The Cumulative Sum Method
One prevalent method involves building upon previous results. The pattern can be expressed as: Result = A + (B × previous result). Here’s how this method unfolds:
- 1 + 4 = 5 (first result, taken as given)
- 2 + 5 = ? (calculate: 5 × 5 = 25, then add 2: 25 + 2 = 27)
- 3 + 6 = ? (calculate: 6 × 27 = 162, then add 3: 162 + 3 = 165)
- 5 + 8 = ? (calculate: 8 × 165 = 1320, then add 5: 1320 + 5 = 1325)
This method yields a rapidly growing sequence that may seem extreme. However, it illustrates how a single shift in rule interpretation can lead to dramatically different outcomes. This emphasizes that these puzzles often assess one’s flexibility in thinking rather than just basic arithmetic capabilities. Solving math puzzles becomes an exercise in adaptability, where solvers must be willing to step outside their comfort zones and embrace unconventional approaches.
2. The “Add and Multiply” Rule
Another interpretation of the puzzle employs the following approach: Result = (A × B) + A. Breaking it down step by step yields:- 1 + 4 = (1 × 4) + 1 = 4 + 1 = 5
- 2 + 5 = (2 × 5) + 2 = 10 + 2 = 12
- 3 + 6 = (3 × 6) + 3 = 18 + 3 = 21
- 5 + 8 = (5 × 8) + 5 = 40 + 5 = 45
This approach is often cited as the most “correct” answer, especially by those who prefer clear mathematical formulas. It provides a logical and repeatable explanation of the pattern, producing results that align consistently with the first three equations. Many puzzle enthusiasts find this solution satisfying and elegant, as it elegantly balances simplicity with creativity. The clarity of this method also serves as a reminder of the structured beauty inherent in mathematics, where rules and patterns can yield consistent results through logical reasoning.